How the Insertion-sort Algorithm Works

Introduction

Usually, I just use library functions/methods of programming languages and do not need to know what happens exactly. Just out of curiosity I sometimes do want to get a better grasp at how something works. To my regret, I often find sources that lack to explain topics in a way that makes understanding it come easy and naturally. Some sources go too deep, some stay too shallow, and some just plain forget to explain important parts of a step. For this reason, I will try to explain such a topic myself in a way that hopefully does a better job at it. This is not a mathematical explanation, but rather an explanation of the working of the insertion-sort algorithm.

The problem

Given an array of numbers (e.g. [4,1,7,9,2,16,15]), we want to sort them in an ascending way, so that the end result will be: [1, 2, 4, 7, 9, 15, 16]

A written-out Approach

1. We start with the second number in the list (array index 1), and from that point we iterate over each next item in the array.
2. From each start point in the iteration, we iterate in a backwards fashion over the array.
3. If the number from our backward iteration is bigger than our start number, we move it a position to the right in the array.
4. We put our start number in the place where the last number moved away from. (Or if nothing moved, we put the number back where it was)

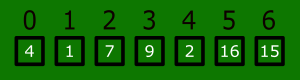
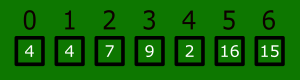
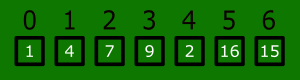
First iteration

Let’s go over step 1 to 4 again.

1. We start with number 1 in the list, which is at array index 1. We memorize this number.
2. We go backwards one step from our starting position, which is number 4, at array index 0.
3. The number 4 is bigger than the number 1, so we copy the number 4 to the array position of the number 1. In the first iteration, there is only one number to the left hand side of number one, thus the iteration stops here.
4. Number 1 will be put in array index 0.

Pseudo code

for array index 1 to array length
{
    memorize = array index value
    
    previous_index = array index - 1

    while (previous_index >= 0) AND (value of previous_index > memorize value)
    {
        copy previous_index value to memorize index
        previous_index -= 1 (go to next previous index)
    }

    copy memorize value to array previous_index + 1 
}

Or shorter:

for i = 1 in array.length
    mem = array[i]
    p = i - 1
    while p >= 0 and array[p] > mem
        array[p+1] = array[p]
        p = p - 1
    array[p+1] = mem

Graphical first iteration

Python Code

numbers = [4,1,7,9,2,16,15]

def insertion_sort():

    for i in range(1, len(numbers)):
        mem = numbers[i]
        p = i - 1

        while p >= 0 and numbers[p] > mem:
            numbers[p+1] = numbers[p]
            p -= 1

        numbers[p+1] = mem

print(numbers)
insertion_sort()
print(numbers)

Python Code with Comments

numbers = [4,1,7,9,2,16,15]

def insertion_sort():

    # loop as many times as there are items, but start at index 1
    for i in range(1, len(numbers)):

        # memorize value of array index
        mem = numbers[i]
        print("memorize number: "+str(mem))
        print("list at start iteration "+str(numbers))

        # get index of previous entry
        p = i - 1

        # while
        # -> p is equal or bigger than 0
        # -> value of index "p" is bigger than memorized value
        while p >= 0 and numbers[p] > mem:

            # set value of index p one place forward, because it is greater
            numbers[p+1] = numbers[p]
            print("copied value "+str(numbers[p])+ " from index "+str(p)+ " to index "+str(p+1))
            # go to next item in a backwards fashion
            p -= 1
            print("list at step            "+str(numbers))

        # set memorized at last moved spot
        numbers[p+1] = mem
        print("copied memorized value " + str(mem) + " to index " + str(p + 1))
        print("list at end iteration   " + str(numbers))
        print("\n")


insertion_sort()

Code output

memorize number: 1
list at start iteration [4, 1, 7, 9, 2, 16, 15]
copied value 4 from index 0 to index 1
list at step            [4, 4, 7, 9, 2, 16, 15]
copied memorized value 1 to index 0
list at end iteration   [1, 4, 7, 9, 2, 16, 15]

memorize number: 7
list at start iteration [1, 4, 7, 9, 2, 16, 15]
copied memorized value 7 to index 2
list at end iteration   [1, 4, 7, 9, 2, 16, 15]

memorize number: 9
list at start iteration [1, 4, 7, 9, 2, 16, 15]
copied memorized value 9 to index 3
list at end iteration   [1, 4, 7, 9, 2, 16, 15]

memorize number: 2
list at start iteration [1, 4, 7, 9, 2, 16, 15]
copied value 9 from index 3 to index 4
list at step            [1, 4, 7, 9, 9, 16, 15]
copied value 7 from index 2 to index 3
list at step            [1, 4, 7, 7, 9, 16, 15]
copied value 4 from index 1 to index 2
list at step            [1, 4, 4, 7, 9, 16, 15]
copied memorized value 2 to index 1
list at end iteration   [1, 2, 4, 7, 9, 16, 15]

memorize number: 16
list at start iteration [1, 2, 4, 7, 9, 16, 15]
copied memorized value 16 to index 5
list at end iteration   [1, 2, 4, 7, 9, 16, 15]

memorize number: 15
list at start iteration [1, 2, 4, 7, 9, 16, 15]
copied value 16 from index 5 to index 6
list at step            [1, 2, 4, 7, 9, 16, 16]
copied memorized value 15 to index 5
list at end iteration   [1, 2, 4, 7, 9, 15, 16]

Conclusion

I tried to give a direct and clear insight to how the insertion-sort algorithm works, without omitting any in-between steps. The algorithm moves from left to right in the outer loop and from right to left in each outer loop to sort the numbers in the array.

References

Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms, third edition. http://portal.acm.org/citation.cfm?id=1614191

Bhargava, A. (2016). Grokking Algorithms: An illustrated guide for programmers and other curious people. https://dl.acm.org/citation.cfm?id=3002869